lunes, 29 de septiembre de 2014
Reglas de ajedrez
REGLAMENTO DEL AJEDREZ
Jugadores: Dos.
Requiere:
Tablero cuadrado 8x8 de 64 casillas con colores alternados (típicamente blanco y negro).
Dos sets iguales de 16 piezas cada uno, uno de piezas blancas y otro negras.
Objetivo:
Dar jaque mate al Rey contrario.
Mecánica:
Por turnos, comenzando por las Blancas, con exactamente un movimiento por turno y con una posición inicial de las piezas fija, hasta que algún jugador consigue el objetivo, se rinde o se produce una situación de empate (tablas). No se puede pasar ni mover más de una vez en ningún caso.
Especificaciones:
Ambos jugadores están colocados enfrentados y separados por el tablero, que debe colocarse entre ellos de forma que la casilla de la esquina derecha más cercana de cada jugador sea blanca. Cada una de las líneas horizontales se llamarán filas y las verticales columnas.
Las casillas suelen identificarse mediante coordenadas de la siguiente forma: una letra [a..h] para la columna seguido de un número [1..8] para la fila, y tomando como origen la esquina inferior izquierda del jugador con Blancas.
Cada jugador tiene a su disposición un grupo de 16 piezas del mismo color con nombres y características determinadas que representa su ejército. El jugador puede en su turno mover piezas sólo de su ejército atendiendo a las normas legales del movimiento en particular. Además cada pieza tiene la habilidad de capturar piezas enemigas, que son retiradas del tablero.
Las 16 piezas de cada ejército están formadas por:
1Rey
1Dama
2 Alfiles
2 Caballos
2 Torres
8 Peones
La disposición inicial de las piezas en la partida es:
Los 8 Peones ocupan las ocho casillas de la segunda fila de cada jugador.
Las 2 Torres ocupan las esquinas de la primera fila.
Junto a las Torres se ubican los Caballos y después los Alfiles.
En las casillas centrales de la primera fila se ubican el Rey y la Dama de forma que el color de la Dama coincida con el de la casilla.
Fig. 1 Posición inicial de las piezas en el tablero.
Movimientos:
Todo movimiento que realice un jugador en su turno debe respetar siempre estas máximas, que se consideran prioritarias:
Ninguna pieza puede salir del tablero, ni haber dos en la misma casilla.
Un jugador no puede capturar piezas de su propio ejército.
No se puede hacer un movimiento tal que deje al final del turno el propio Rey en jaque, es decir, que el rival pudiera capturarlo en su turno.
Cada tipo de pieza mueve de la siguiente forma (ordenado por sencillez):
Torre:
Movimiento: todas las casillas que se deseen por la misma fila o columna de la original, con límite el final del tablero o la primera pieza encontrada en el camino. Si la pieza es enemiga, está dentro del rango.
Captura: si una pieza enemiga es alcanzable, se puede capturar colocando la torre en la casilla ocupada por la pieza enemiga y retirando ésta del tablero.
Alfil:
Movimiento: todas las casillas que se deseen por una de las cuatro diagonales que parten de la pieza, hasta el final del tablero o la primera pieza encontrada. Si la pieza es enemiga, está dentro del rango.
Captura: se coloca el Alfil en la casilla ocupada por la pieza rival, y ésta se retira.
Nótese que cada uno de los alfiles comienza en casillas de distinto color, y que no pueden alcanzar las de color contrario.
Dama (Reyna):
Movimiento: funciona como una Torre y un Alfil combinados, es decir, en cualquiera de las 8 direcciones posibles todas las casillas deseadas, hasta el final del tablero o la primera pieza encontrada. Si es rival, está dentro del rango.
Captura: se coloca la Dama en la casilla ocupada por la pieza rival retirando ésta del tablero.
Rey:
Movimiento: funciona como la Dama pero sólo una casilla por vez, es decir, sólo puede desplazarse a casillas adyacentes.
Captura: cualquier pieza enemiga situada en alguna de las 8 casillas adyacentes puede ser capturada, situando el Rey en ella y retirando la pieza enemiga.
Nótese que en particular implica que el Rey no puede desplazarse al lado del otro, pues quedaría a su vez atacado por el rival.
Caballo:
Movimiento: puede moverse a una de las 8 casillas que están ubicadas a una cierta distancia suya, sin importar las piezas que pudieran haber en medio. Cada una de estas casillas destino forman una figura de “L” desde la casilla inicial. Todas ellas son de distinto color de la inicial.
Fig. 2 Casillas destino de un caballo.
Captura: toda pieza enemiga situada en una casilla destino de un Caballo, sin importar las que haya en medio, puede ser capturada desplazándolo allí y retirando la capturada.
Peón:
Movimiento: hacia delante, en la misma columna, una casilla por vez. Si es la primera vez que ese peón es movido (aún se halla en la segunda fila) puede desplazarse 1 o 2 casillas.
Captura: a diferencia del resto de piezas, no capturan como se mueven. Cada Peón ataca las dos casillas que están en diagonal hacia delante, de forma que al capturar cambian de columna. Cualquier pieza enemiga que se ubique en estas casillas atacadas puede ser capturada.
Además, un Peón dispone de una forma adicional para capturar peones enemigos en una determinada circunstancia (captura al paso). Para ello:
El peón original debe estar en su quinta fila.
El peón rival debe estar en su posición inicial en una columna adyacente.
El rival debe avanzar dos pasos su peón, de modo que ambos peones quedan juntos en la misma fila.
En ese momento, si el jugador quiere, puede capturar al enemigo como si éste sólo se hubiera movido una casilla, es decir, desplazando el propio en diagonal a la fila siguiente y retirando al capturado. Si decide ignorar la captura en ese turno perderá el derecho a hacerlo.
Es la única captura del juego en la que la pieza que captura no acaba en la casilla de la capturada.
Coronación: cuando un peón llega a la última fila ha de ser cambiado (coronado) por un Caballo, Alfil, Torre o Dama, aunque el jugador ya posea esa pieza. De esta forma se puede incrementar la propia fuerza al poder disponer, por ejemplo, de varias Damas. Esta sustitución está incluida en el mismo turno del peón.
Un movimiento especial: el enroque
El enroque es la única jugada en la que en el mismo turno se mueven dos piezas propias: el Rey y una Torre. Este movimiento sólo puede hacerlo cada jugador 1 vez en toda la partida, siendo opcional pero cumpliendo una serie de requisitos, uno de ellos que lo imposibilitaría definitivamente y otros sólo temporalmente:
Debe ser el primer movimiento tanto del Rey como de la Torre a enrocar. Si se mueve el Rey, el enroque queda imposibilitado para el resto de la partida. Si se mueve la Torre, aún es posible usar la otra.
No debe haber ninguna pieza entre el Rey y la Torre, ni amiga ni contraria.
El Rey no puede estar en jaque (atacado) en ese momento, ni su casilla destino, ni la intermedia. Otras casillas, como la origen de la Torre, si pueden estarlo.
El movimiento se efectúa en este orden sea cual sea el lado por el que se enroque: primero se desplaza el Rey dos casillas hacia la Torre y después se mueve la Torre a la casilla adyacente al otro lado del Rey.
Fig. 3 Posibles enroques del Blanco
Jaque:
Se dice que un jugador está en jaque cuando su Rey está siendo atacado por una o dos piezas enemigas, y sería posible para el rival el capturarlo al siguiente turno. No es obligatorio anunciar explícitamente el jaque. Siguiendo las normas, el jugador debe actuar en consecuencia de forma que esa situación desaparezca en su turno. Para ello puede:
Capturar la pieza que ataca, si dispone de alguna pieza que lo haga, y sólo hay una pieza atacando.
Poner una pieza en el medio a modo de escudo, si la pieza que ataca no es un Caballo y no hay más de una atacando.
Mover el Rey a una casilla tal que deje de estar en jaque, si hay.
Fig. 4 Ejemplo de jaque con una pieza Fig. 5 Ejemplo de jaque doble
Jaque mate:
Cuando se produce un jaque y un jugador no puede ejecutar ningún movimiento que le permita resolver esa situación, ha perdido la partida.
Tablas
Existen muchas posibilidades de acabar una partida en tablas:
Un jugador que no está en jaque no puede mover en su turno (ahogado).
Ambos jugadores han acordado las tablas.
Se ha producido la repetición de la misma posición 3 veces (no con los mismos movimientos necesariamente, pero sí con las mismas piezas y los mismos posibles movimientos para ambos bandos).
No existen suficientes piezas por ningún bando para forzar un jaque mate. Si aún queda algún peón, no se aplica. Casos posibles: Rey contra Rey, Rey contra Rey y Caballo o Alfil.
Se produce una secuencia de 50 jugadas de cada bando seguidas sin captura o movimiento de peón.
domingo, 21 de septiembre de 2014
domingo, 14 de septiembre de 2014
lunes, 8 de septiembre de 2014
Todo sobre potencias
Multiplicar potencias de distinta base y distinto exponente
¿Qué son las potencias?
Las potencias están formadas por una base y un exponente. El exponente nos indicará cuántas veces debemos multiplicar la base por sí misma.
Índice de Temas:
- Tipos de potencias según su base
Propiedades de las potencias
- Multiplicación y división de potencias
- Decimales:
producto de un número natural y una potencia de 10
Tipos de potencias según su base
1) Potencias de base natural y exponente natural
En este caso multiplicaremos la base por sí misma las veces que nos indique el exponente.

2) Potencias cuya base es una fracción y su exponente un número natural
El exponente nos indica cuantas veces debemos multiplicar por sí mismos tanto el numerador como el denominador de la fracción.

3) Potencias de base decimal y exponente natural
Multiplicaremos el decimal por sí mismo cuantas veces nos indique el exponente.

Otra manera de resolver una potencia de base decimal, es transformando el decimal a fracción y luego multiplicando la fracción por sí misma las veces que nos indique el exponente.

4) Potencias de base entera y exponente natural
Para resolver estas potencias multiplicaremos el entero por sí mismo las veces que nos indique el exponente.
En el caso de los enteros positivos, se resolverán de la misma manera en que lo hacemos con los números naturales. Pero, ¿que pasará si el entero es negativo?

Como te habrás dado cuenta, cuando estemos frente a potencias cuya base entera sea negativa, el resultado será positivo si el exponente es par y negativo si el exponente es impar.
5) Potencias de base 10
a) Con exponente natural

Como verás, es muy simple resolver potencias de base 10 y exponente natural. El resultado siempre será un 1 acompañado de cuantos ceros nos indique el exponente. Así si tenemos
 , entonces el resultado será un 1 acompañado de 3 ceros, es decir, 1 000.
, entonces el resultado será un 1 acompañado de 3 ceros, es decir, 1 000.b) Con exponente entero
Para resolver potencias de base 10 con exponente entero positivo, el procedimiento será el mismo que utilizamos para resolver potencias de base 10 y exponente natural.
Pero, ¿cómo resolvemos aquellas potencias de base 10 y exponente negativo?

Observando la figura, podemos ver que una forma de resolver potencias de base 10 y exponente negativo es transformar la potencia en una fracción donde el numerador siempre es 1 y el denominador será la misma potencia pero con exponente positivo. Luego al dividir la fracción obtenemos el resultado de la potencia.
Una forma más fácil de resolverlas es la siguiente:
- El resultado siempre será un decimal sin enteros
- El exponente negativo nos indicará en que posición debemos ubicar el 1 en la parte decimal. Así, el
-1, nos indicará que debemos ubicar el 1 en la primera posición, es decir, los décimos; el -2, nos indica que debemos ubicarlo en la segunda posición, es decir, los centésimos, y así sucesivamente
- Y por último, todos los espacios que queden vacíos a la izquierda del 1 en la parte decimal debemos rellenarlos con ceros
Veamos el siguiente ejemplo:

Importante:
Todas las potencias con base distinta de 0 cuyo exponente sea 0, su resultado será siempre 1.

Propiedades de las potencias
1) Multiplicación de potencias de igual base
Al multiplicar potencias de igual base, mantendremos la base y sumaremos los exponentes.

2) División de potencias de igual base
Cuando queremos dividir potencias de igual base, mantendremos la base y restaremos los exponentes.

3) Potencia de una potencia
Para resolver la potencia de una potencia, debemos mantener la base y multiplicar los exponentes.

4) Multiplicación de potencias de igual exponente
Para obtener el producto de potencias de igual exponente, debemos multiplicar las bases y mantener el exponente.

5) División de potencias de igual exponente
Para obtener el cuociente de potencias de igual exponente, debemos dividir las bases y mantener el exponente.

Como te habrás dado cuenta, las propiedades de las potencias son aplicables a bases naturales, fraccionarias, decimales y enteras.

Como te habrás dado cuenta, las propiedades de las potencias son aplicables a bases naturales, fraccionarias, decimales y enteras.
Decimales: producto de un número natural y una potencia de 10
Los decimales podemos representarlos como la multiplicación entre un número natural y una potencia de 10 con exponente entero negativo.
Veamos los siguientes ejemplos:

¿Qué resultados obtenemos?

Como podrás darte cuenta, todo número decimal puede ser representado como el producto de un número natural por una potencia de 10 con exponente negativo.
Veamos los siguientes ejemplos:

¿Qué resultados obtenemos?

Como podrás darte cuenta, todo número decimal puede ser representado como el producto de un número natural por una potencia de 10 con exponente negativo.
¿Cómo podemos representar el decimal 12,3?

¿Cómo lo hicimos?
Al decimal 12,3, le corrimos la coma un espacio a la derecha de manera que quedara escrito como número natural 123,0 = 123 y luego nos preguntamos cuántos espacios debíamos correr la coma a la izquierda para que volviéramos a obtener el decimal 12,3. Como nos tenemos que correr 1 espacio, entonces el exponente de la potencia de 10 será -1.
También podríamos representarlo de las siguientes formas:

Multiplicación y división de potencias
1) Multiplicación y división de una potencia de 10 por una potencia de 10
Para resolver una multiplicación o división de una potencia de 10 por otra potencia de 10, primero debemos recurrir a las propiedades de las potencias que nos dicen que al multiplicar dos potencias de igual base, debemos mantener la base y sumar los exponentes y que al dividir, debemos mantener la base y restar los esponentes.
Luego debemos resolver la potencia como aprendimos anteriormente: el resultado será un 1 acompañado de cuantos ceros nos indique el exponente.
2) Multiplicación y división de un número natural por una potencia de 10
El producto entre un número natural y una potencia de 10 será el número natural acompañado de cuantos ceros nos indique la potencia de 10.

En el caso de la división, primero debemos recordar que un número natural es un decimal con período cero, por lo tanto, es lo mismo decir 45 que 45,0. Para obtener el cuociente debemos mantener el número natural y correr la coma hacia la izquierda las veces que nos indique el exponente de la potencia de 10. Si quedan espacios vacíos como en el primer ejemplo, debemos rellenarlos con ceros.


En el caso de la división, primero debemos recordar que un número natural es un decimal con período cero, por lo tanto, es lo mismo decir 45 que 45,0. Para obtener el cuociente debemos mantener el número natural y correr la coma hacia la izquierda las veces que nos indique el exponente de la potencia de 10. Si quedan espacios vacíos como en el primer ejemplo, debemos rellenarlos con ceros.

3) Multiplicación y división de un número decimal por una potencia de 10

Al multiplicar un decimal por una potencia de 10, debemos correr la coma hacia la derecha cuantas veces nos indique el exponente de la potencia de 10; en el caso de las divisiones, debemos correr la coma hacia la izquierda.
Cuando sea necesario debemos agregar ceros después de la última cifra de la parte decimal, en el caso de las multiplicaciones; y anteponer ceros a la primera cifra de la parte decimal o en la parte entera en el caso de las divisiones.
PROPIEDAD DEL PRODUCTO DE POTENCIAS
Como simplifica 72 × 76?
Si Usted recuerda la forma de como son definidos los exponentes, Usted sabe que esto significa:
(7 × 7) × (7 × 7 × 7 × 7 × 7 × 7)
Si elimina los paréntesis, tenemos el producto de ocho 7s, que puede ser escrito más simplemente como:
78
Esto sugiere un atajo: todo lo que necesitamos hacer es sumar los exponentes!
72 × 76 = 7(2 + 6) = 78
En general, para todos los números reales a, b, y c,
ab × ac = a(b + c)
Para multiplicar dos potencias con la misma base, sume los exponentes.
Si Usted solo recuerda esta y olvida el resto, puede usarla para encontrar la mayoría de las otras propiedades.
EXPONENTES CERO
Muchos estudiantes que inician piensan que es raro que algo elevado a la potencia de cero es 1. (“Debe ser 0!”) Puede usar la propiedad del producto de potencias para mostrar porque esto debe ser verdadero.
70 × 71 = 7(0 + 1) = 71
Sabemos que 71 = 7. Así, esto nos dice que 70 × 7 = 7. Que número por 7 es igual a 7? Si decimos que 0, tenemos 0 × 7 = 7. No es verdadero.
En general, para todos los números reales a, a ≠ 0, tenemos:
a0 = 1
Dese cuenta que 00 no está definido. (Presione aquí para ver porque.)
EXPONENTES NEGATIVOS
Puede usar la propiedad del producto de potencias para encontrar esta también. Suponga que desea saber cuanto es 5-2.
5-2 × 52 = 5(-2 + 2) = 50
Sabemos que 52 = 25, y sabemos que 50 = 1. Así, esto nos dice que 5-2 × 25 = 1. Que número por 25 es igual a 1? Ese sería su inverso multiplicativo, 1/25.
En general, para todos los números reales a y b, donde a ≠ 0, tenemos:
PROPIEDAD DEL COCIENTE DE POTENCIAS
Cuando multiplica dos potencias con la misma base, Usted suma los exponentes. Así cuando divide dos potencias con la misma base, Usted resta los exponentes. En otras palabras, para todos los números reales a, b, y c, donde a ≠ 0,
Lo que realmente está haciendo es eliminar los factores comunes del numerador y del denominador. Ejemplo:
PROPIEDAD DE POTENCIA DE UN PRODUCTO
Cuando multiplica dos potencias con el mismo exponente, pero bases diferentes, las cosas se hacen un poco de forma distinta.
32 × 42 = (3 × 3) × (4 × 4)
Debido a las propiedades conmutativa y asociativa de la multiplicación, podemos reescribir esto como
32 × 42 = (3 × 4) × (3 × 4) = 122
En general, para todos los números reales a, b, y c (mientras que tanto a y c o tanto b y cno sean cero):
ac × bc = (ab)c
Para encontrar la potencia de un producto, ya sea que encuentre la potencia de cada factor y luego multiplique o multiplique los factores y eleve a la potencia el producto.
PROPIEDAD DE POTENCIA DE UN COCIENTE
Esta es bastante similar a la anterior. Por la eliminación de factores comunes, puede ver que:
Ejemplo 1:
Ejemplo 2:
Simplifique
Para todos los números reales a, b, y c (siempre que b ≠ 0, y a y c ambas no sean 0):
PROPIEDAD DE POTENCIA DE UNA POTENCIA
La propiedad del producto de potencias puede ser desarrollada. Suponga que tiene un número elevado a una potencia, y multiplica la expresión completa por si misma una y otra vez. Esto es lo mismo que elevar la expresión a una potencia:
(53)4 = (53)(53)(53)(53)
Pero la propiedad del producto de potencias nos dice que
(53)(53)(53)(53) = 53 + 3 + 3 + 3 = 54(3) = 512
Así es suficiente con solo multiplicar las potencias!
En general, para todos los números reales a, b, y c,
(ab)c = abc.
Para encontrar una potencia de una potencia, multiplique los exponentes.
EXPONENTES RACIONALES
Hemos cubierto los exponentes positivos, exponentes negativos, y los exponentes cero. Pero que pasa si tiene un exponente que no es un entero? Que pasa, por ejemplo, si 91/2?
Podemos volver a caer otra vez en la propiedad del producto de potencias para encontrar:
91/2 × 91/2 = 9(1/2 + 1/2) = 91
Sabemos que 91 = 9, así 91/2 = . Así, el exponente ½ trabaja como una raíz cuadrada. Similarmente, a1/3 es equivalente a .
lunes, 1 de septiembre de 2014
Ley de los signos
Ley de los signos
Suma
1. Si los números tienen el mismo signo se suman se deja el mismo signo.
3 + 5 = 8
(−3) + (−5) = − 8
2. Si números tienen distinto signo, se restan y al resultado se le coloca el signo del número con mayor valor absoluto.
−3 + 5 = 2
3 + (−5) = − 2
Multiplicación y división
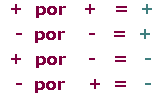
2 · 5 = 10
(−2) · (−5) = 10
2 · (−5) = − 10
(−2) · 5 = − 10
10 : 5 = 2
(−10) : (−5) = 2
10 : (−5) = − 2
(−10) : 5 = − 2
Potencias
1. Las potencias de exponente par son siempre positivas.
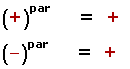
26 = 64
(−2)6 = 64
2. Las potencias de exponente impar tiene el mismo signo de la base.
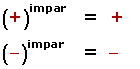
23 = 8
(−2)3 = −8
Juegos matemáticos para principiantes
Les recomiendo entren a esta página interactiva (a algunos les parecerán muy sencillos los juegos, pero por algo se empieza). Se aceptan sugerencias.
Denle click
http://www.juegoseducativosvindel.com/index.php
Denle click
http://www.juegoseducativosvindel.com/index.php
Suscribirse a:
Comentarios (Atom)